
In a groundbreaking development, US mathematicians have transformed what was once considered “useless” mathematics into a pivotal breakthrough in quantum computing. These mathematical principles, previously dismissed as theoretical exercises, are now set to revolutionize the field of quantum technology and computation. This newfound applicability underscores the importance of theoretical research and opens up new avenues for technological advancement.
The Evolution of Mathematical Theory
Tracing the journey of mathematical theories deemed impractical reveals a rich tapestry of intellectual exploration. Historically, many mathematical concepts were developed without a clear application in mind. For instance, number theory, which was once considered a purely theoretical pursuit, found its place in modern cryptography. Similarly, complexity theory, once seen as an abstract discipline, has become essential in addressing contemporary computational challenges.
Complexity theory plays a crucial role in understanding the limits of computation and the resources required to solve problems. As we push the boundaries of what computers can achieve, these theories become increasingly relevant. They provide a framework for evaluating algorithms and understanding the inherent difficulty of computational tasks. The transition from theoretical to practical applications in this domain illustrates the often-underestimated potential of abstract mathematics.
Bridging theoretical and applied mathematics involves recognizing the potential of abstract concepts to address real-world problems. This transition is not always straightforward, but it is facilitated by interdisciplinary collaboration. By fostering communication between mathematicians, computer scientists, and engineers, abstract theories can be translated into tangible solutions. This synergy has paved the way for breakthroughs in fields like cryptography, optimization, and now, quantum computing.
Quantum Computing: The Next Frontier

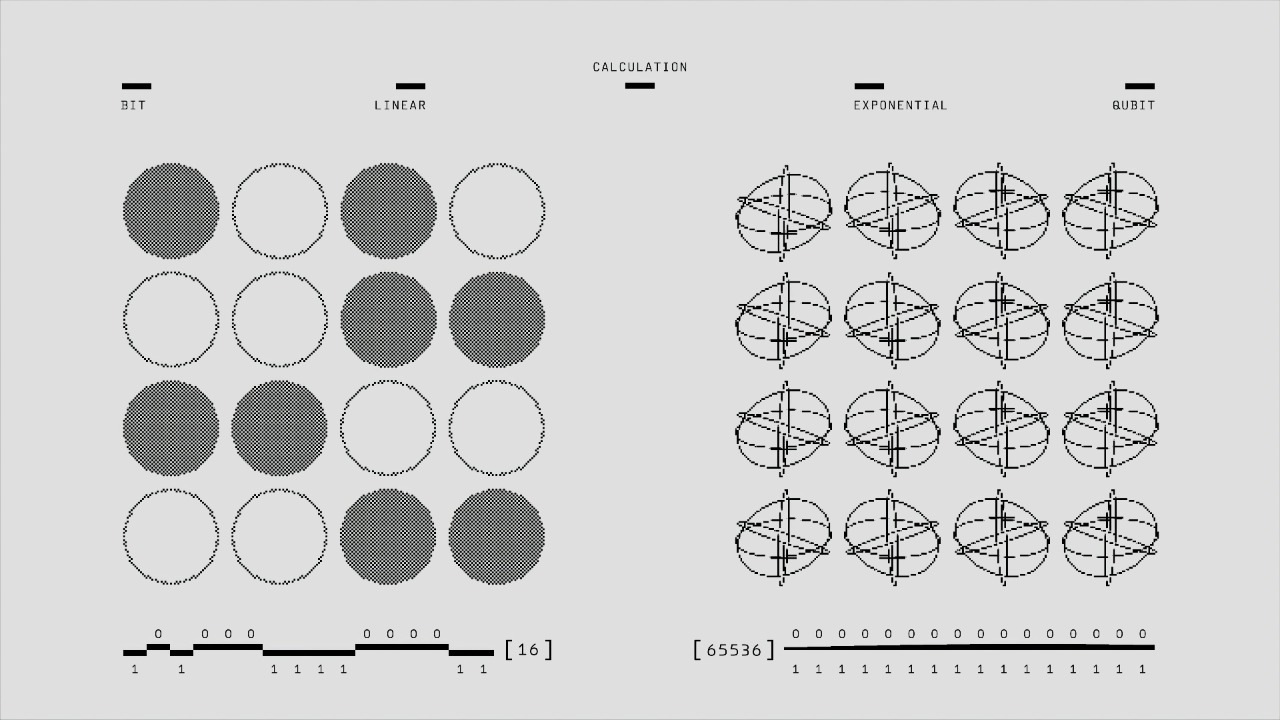
Quantum computing represents the next frontier in computational technology. At its core are concepts such as qubits, superposition, and entanglement, which differ fundamentally from classical computing paradigms. In a quantum system, qubits can exist in multiple states simultaneously, enabling the processing of vast amounts of data at unprecedented speeds.
Despite the promise of quantum computing, classical computing methods face significant limitations in quantum scenarios. Traditional computers rely on binary systems, which can only process information in a sequential manner. This constraint makes it difficult to tackle complex problems that require simultaneous consideration of multiple variables, such as those found in quantum mechanics or complex optimization tasks.
The quest for quantum supremacy, the point at which quantum computers can perform tasks beyond the reach of classical computers, is a driving force in current research. Although significant progress has been made, challenges remain. Issues such as error correction, decoherence, and the scalability of quantum systems need to be addressed to fully realize the potential of quantum computing. Nevertheless, the integration of mathematical breakthroughs into this domain offers promising pathways to overcome these hurdles.
Transforming ‘Useless’ Math into Quantum Solutions

The transformation of “useless” math into quantum solutions is a testament to the innovative spirit of interdisciplinary research. Key mathematical concepts, once relegated to theoretical exercises, are now crucial for quantum computing. For example, the study of topological phases of matter, initially considered an esoteric topic, has become vital in understanding and developing robust quantum systems.
An interdisciplinary approach has been instrumental in this transformation. Collaborations between mathematicians, physicists, and computer scientists have allowed for a cross-pollination of ideas, leading to breakthroughs that would have been impossible in isolation. By drawing on diverse expertise, researchers have been able to tackle complex problems from multiple angles, accelerating advancements in quantum technology.
Specific case studies highlight the impact of these mathematical principles on quantum technology. For instance, the use of error-correcting codes, derived from abstract algebra, has proven essential in addressing the issue of noise in quantum systems. Similarly, algorithms based on linear algebra have been adapted to optimize quantum computations, demonstrating the practical applications of formerly theoretical concepts.
Implications for Technology and Society

The implications of these advancements extend far beyond the realm of technology. Quantum computing holds the potential to revolutionize various industries, from cryptography to materials science. In cryptography, quantum algorithms offer new methods for secure communication, challenging existing encryption techniques and prompting the development of quantum-resistant protocols.
In materials science, quantum simulations can model complex molecular interactions, leading to the discovery of new materials with enhanced properties. This capability has applications in areas such as drug discovery, where understanding molecular dynamics is crucial for developing effective treatments. The ability to simulate these interactions at a quantum level opens up new possibilities for scientific research and innovation.
However, the rise of quantum technologies also raises ethical considerations. As these systems become more powerful, questions about their use and potential misuse arise. Ensuring that quantum technologies are developed and deployed responsibly is essential to maximizing their benefits while minimizing risks. This requires a proactive approach to ethics, involving stakeholders from various sectors to navigate the implications of these powerful tools.
Challenges and Future Directions

Despite the promising advancements in quantum computing, several challenges remain. Technical hurdles such as error correction and maintaining coherence over extended periods are significant obstacles that researchers must overcome. Additionally, theoretical challenges persist, as the full potential of quantum algorithms and their applications are not yet fully understood.
The role of education and research is critical in preparing the next generation of scientists and mathematicians to tackle these challenges. By fostering an environment that encourages curiosity and interdisciplinary collaboration, educational institutions can equip students with the skills and knowledge necessary to advance quantum research. Initiatives that promote STEM education and support early-career researchers are vital to sustaining progress in this field.
Global collaboration is also essential in advancing quantum research. As the field evolves, international partnerships can facilitate the sharing of knowledge and resources, accelerating discoveries and fostering innovation. By working together, researchers can overcome the limitations of individual efforts and drive the development of quantum technologies to new heights.